|
Med BETONexpress kan en enkelt
utføre beregninger og analyser av betongelementer i henhold til Eurokode 2 (EC2). I
tillegg benyttes Eurocode 7 for geotekniske analyser (fundament, støttemurer), Eurocode 1
for lastkombinasjoner og Eurocode 8 for seismiske beregninger.
Materialegenskaper og beregningsparametre kan justeres ifølge krav
til Nasjonalt anvendelsesdokument, NA. Enkelt spesifiseres nødvendige dimensjoner, laster og parametre for konstruksjonsobjektet og beregningene utføres samtidig. Forhåndsvalgte
verdier og kontroll av feilaktige input verdier forenkler prosessen. Rapporten som produseres viser i detalj alle kalkulasjoner og
beregninger trinnvis med referanse til korresponderende beregningsregler.
Bøyelister produseres samtidig, og ved hjelp av editor kan en legge til eller fjerne
armering.
Et
innholdssensitivt Hjelp system, veileder deg gjennom bruken av programmet og Eurokode
reglementet.
Online brukermanual er inkludert i
programvaren. I tillegg er en meny med ingeniørverktøy inkludert: Omdannelse
av enheter, tverrsnittsegenskaper, arealberegninger, egenskaper armeringsstål,
jordtrykkskoeffisienter. |
|
Utfører beregninger med eurokodene enkelt og oversiktlig med
referanser til regelverket. |
|
 |
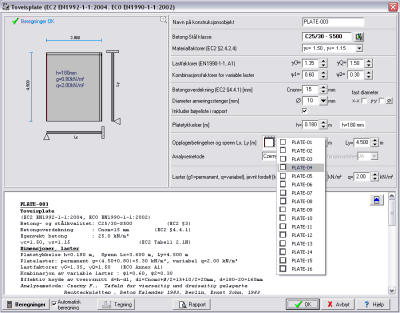
 Betongplater Betongplater
Tverrsnitt
av plate i bøyning.
Beregninger av platetverrsnitt for massive plater og ribbeplater utsatt for bøyemoment.
Toveisplater.
Tre kategorier av toveisplater er inkludert. Plater understøttet på alle fire sider
(fritt opplegg eller innspenning), plater understøttet på tre sider, eller plater
understøttet på to tilstøtende sider. Opplagerbetingelser kan spesifiseres for hver
plateside. Marcus' metode eller tabeller for lineære analyser er benyttet for beregninger
av bøyemoment.
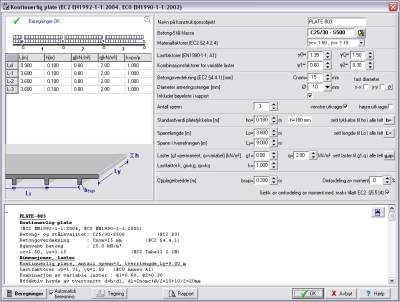
Enveis
kontinuerlige plater.
Beregninger av enveis kontinuerlige plater opp til 8 spenn, med mulige utkragerplater og
jevnt fordelte laster (permanente og variable). Spennlengde, platetykkelse og last kan
spesifiseres for hvert spenn. Statiske beregninger er utført med elementmetode, der
det er tatt hensyn til de minst gunstige plassering av variable laster på felt for
å
oppnå maks. og min. verdier for bøyemoment. Momentet i opplager er beregnet i ytterkant
av opplager. Momentet kan modifiseres ved omfordeling av moment, Eurocode 2 §5.5.
Utkragerplater.
Beregninger av utkragerplater med variabel tykkelse. Jevnt fordelt last og konsentrert
last (permanent og variabel) på fri ende kan spesifiseres.
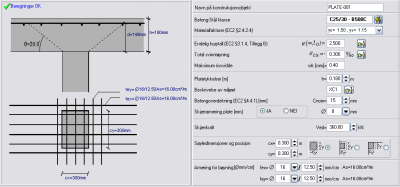
Flatdekker,
Skjærkraft fra konsentrerte laster (2015)
Dimensjonering av platetverrsnitt
for skjær fra konsentrert lastinnføring i henhold til Eurocode
2, § 6.4. Kontroll av skjærkapasitet i kontrollsnitt rundt
belastede flater. Dersom vEd er større enn verdien vrd,c, i det
aktuelle kontrollsnittet, beregner programmet skjærarmering i
henhold til Eurocode 2, § 6.4.5.
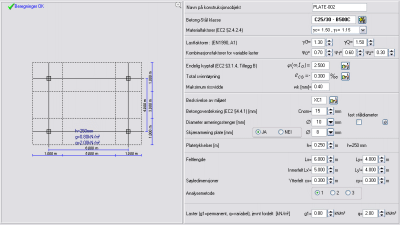
Dimensjonering
av flatdekke
(2015)
Dimensjonering av flatdekke med innerfelt dimensjoner Lx og Ly, og ytterfelt dimensjoner Lx’ og
Ly’.
Spesifiser med JA eller NEI om du ønsker å bruke skjærarmering
eller ikke. Dersom JA, vil skjærarmering beregnes hvis βVEd>Vrd,c,. Beregningen av moment og skjærkraft er basert på
koeffisienter av kontinuerlig bjelke.
Dersom beregningene ikke godkjennes i henhold til Eurokodene,
vil du få beskjed om f.eks. å øke tykkelse på plate.
Momentkapasitet. Momentkapasitet
av platetverrsnitt med spesifisert armering.
Momentkapasitet med FRP forsterkning.
Momentkapasitet
av platetverrsnitt med spesifisert armering og forsterkning med FRP (Fiber armerte
polymerer).
Lettbetong (LWAC) Solid og ribbeplater
Armering mot bøyning er beregnet i
henhold til Eurocode 2, § 6.1, i bruddgrensetilstand for bøyning.
Rissviddebegrensning og nedbøyningsbegrensning beregnes i henhold
til Eurocode 2 §7.3, §7.4 i bruksgrensetilstander (SLS). Armeringens
minimumskrav er ifølge Eurocode 2, §8, §9. |
|
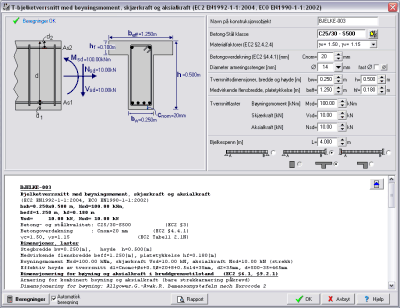
 Bjelker Bjelker
Bjelketverrsnitt.
Beregninger av rektangulære- eller T-bjelketverrsnitt utsatt for kombinert bøyning og
skjær.
Torsjon.
Beregninger av rektangulære- eller T-bjelketverrsnitt utsatt for kombinert torsjon,
skjær og bøyning.
Bjelke
over ett felt med kombinert last.
Beregninger av
ettfeltsbjelker med kombinert last. Bjelketverrsnitt kan være rektangulært, T-formet,
eller ensidig T-bjelke.
Medvirkende
flensbredde er evaluert i henhold til Eurocode 2 §5.3.2.
Venstre og/eller høyre
opplagerbetingelser for bjelken kan spesifiseres som fritt opplagret eller innspent
opplager.
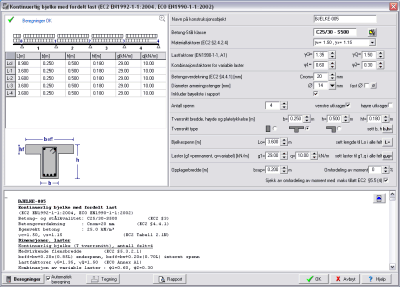
Kontinuerlig
bjelke over flere felt. Beregninger av
kontinuerlige bjelker, opp til 8 felt med mulige utkragerplater og
jevnt fordelte laster.
De statiske beregninger er utført med elementmetode, der det er tatt hensyn til de
minst gunstige plassering av variable laster på felt for a oppnå maks. og min. verdier
for bøyemoment og skjærkraft.
Momentet kan modifiseres ved
omfordeling av moment, Eurocode 2, EC2 § 5.5,
Momentkapasitet.
Evaluering av momentkapasitet
for
bjelketverrsnitt med gitt armering.
Momentkapasitet
med FRP
forsterkning. Evaluering av momentkapasitet for bjelketverrsnitt med gitt armering og
forsterkning med FRP.
Lettbetong (LWAC) Rektangulære
bjelker eller bjelker med T-bjelketverrsnitt
Laster kan være permanente og
variable lastkomponenter. Beregningene av lastkombinasjoner er
henhold til EN 1990:2002. |
|
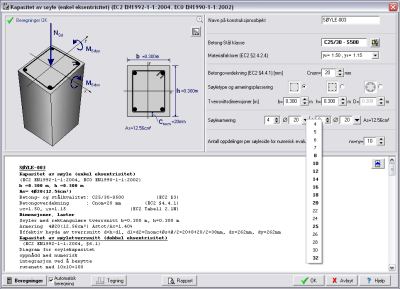
 Søyler Søyler
Rektangulære og runde søyletverrsnitt
med trykk og biaksial bøyning. Dimensjoneringen utføres ved numerisk
integrasjon av betong- og stålkrefter på søylens tverrsnitt. I
tillegg vises beregningsverdier utifra (P-Mx-My) tabeller For
rektangulære søyler velges plassering av armering ( i
hjørner/perimeter).
Enkeltstående staver Beregningene utføres i henhold til
Eurocode § 5.8. Slankhetseffekt og 2.ordensteori (virkning av
stavens forskyvninger) er betraktet i beregningene. Slankhet og
effektive lengd defineres i henhold til § 5.8.3.2. Analysemetoden er
i henhold til § 5.8.7.3., Faktor for økning av moment. Laster er
aksialkraft og bøyemomenter i x-x og y-y retninger.
Slanke trykkstaver med biaksial bøyning. Beregningene utføres
i henhold til Eurocode 2 § 5.8.. Slankhetseffekt og 2.ordensteori
(virkning av stavens forskyvninger) er betraktet i beregningene. For
varierende opplagerbetingelser kan en spesifisere retningen både i x
og y retning (fast innspenning, dreibar innspenning eller fri ende).
For kontinuerlige søyler i rammekonstruksjoner, kan
rotasjonsinnspenningsgraden i endene spesifiseres. Belastningen ar
aksial last og bøyningsmomentet i x-y retning i søyleende.
Tverrsnittskapasitet av rektangulære eller sirkulære søyler
utsatt for trykk og enaksiale moment og trykk og biaksiale moment.
Søylens tverrsnittskapasitet med gitte dimensjoner og armering, er
beregnet med numerisk integrasjon av krefter i trykksone. De indre
krefter i numerisk integrasjon er trykk av betong (parabolisk
tøynings- spenningsdiagram), og trykk og strekk (elastoplastisk
tøynings- spenningsdiagram) av armering i posisjon ved
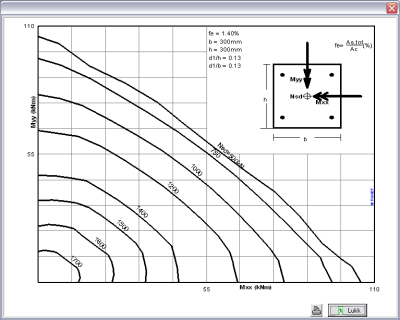
armeringsstenger. Resultatene er verdier i tabeller for
kapasitetsoverflate, Pn-Mn for enaksial bøyning og Pn-Mx-My for
biaksial bøyning.
Tverrsnittskapasitet av rektangulære eller sirkulære søyler med
FRP forsterkning utsatt for trykk og enaksiale moment og trykk
og biaksiale moment. Søylens tverrsnittskapasitet med gitte
dimensjoner, armering og FRP forsterkning, er beregnet med numerisk
integrasjon av krefter i trykksone. De indre krefter i numerisk
integrasjon er trykk av betong (parabolisk
tøynings-spenningsdiagram), trykk og strekk(elastoplastisk
tøynings-spenningsdiagram) av armering i posisjon ved
armeringsstenger, og trykk og strekk av FRP material (lineær
tøynings- spenningsdiagram). Resultatene er verdier i tabeller for
kapasitetsoverflate, Pn-Mn for enaksial bøyning og Pn-Mx-My for
biaksial bøyning. |
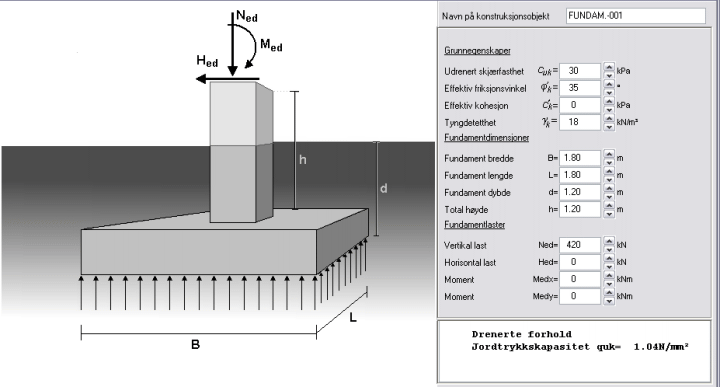 |
Grunnens bæreevne (2015)
Dimensjonering av fundamenter er basert på
grunnens bæreevne.
Den dimensjonerende vertikale bæreevne beregnes
med analytiske eller semi-empiriske metoder.
Tillegg D av Eurocode 7, EN1997:2004 beskriver
en metode for beregning av grunnens bæreevne.
Metodene i Tillegg D for drenerte og udrenerte forhold er inkludert
i programmet. Dimensjonering av grunnens bæreevne er estimert for
grensetilstand, EQU, STR og GEO.
|
|
 |
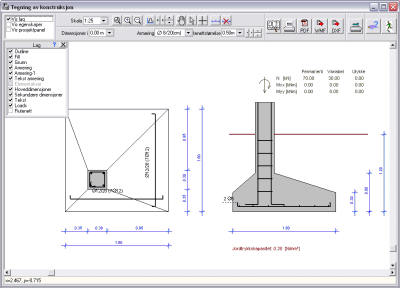
 Søylefundament Søylefundament
Beregninger
av firkantede eller rektangulære fundament, utsatt for vertikal last og moment.
Fundamentene kan være flate eller skrå, sentriske eller eksentriske. Beregninger av
lastkombinasjoner utføres i henhold til Eurocode 2, Eurocode 7 og Eurocode 1.
Eksakt beregning av
trykkfordeling under fundament. Geotekniske beregninger med Eurocode 7.
spenninger. 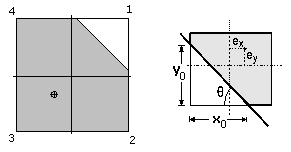
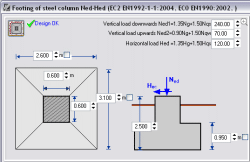
Betongfundamenter for stålsøyler (2015)
Betongfundamenter av stålsøyler må beregnes for
å motstå maksimalt jordtrykk og fundamentet må ha nok vekt for å
hindre oppløft fra vind eller seismiske krefter.
Du kan spesifisere leddet søylefot og
fastinnspent søylefot. Du kan også spesifisere om fundamentet har
stål-strekkbånd for å ta horisontale strekkrefter som virker utover.
|
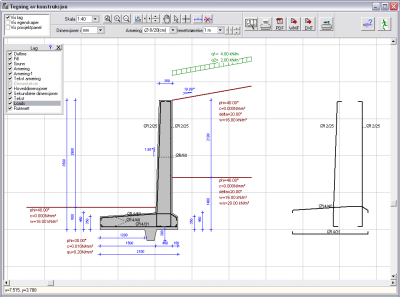 |
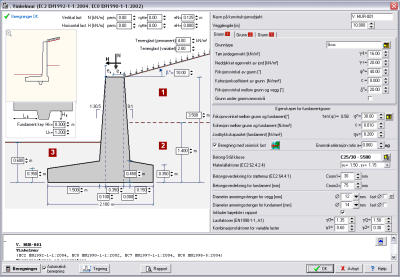
 Støttemurer Støttemurer
- Beregninger av gravitasjonsmurer
av mur eller betong er basert på Beregninger med bruddgrensetilstander i henhold til
Eurocode 6, eller Beregninger med tillatte spenninger.
- Beregninger av vinkelmurer
er basert på Beregninger med bruddgrensetilstander for betong i henhold til Eurocode 2.
Stabilitetskontroll er basert enten på
Beregninger med bruddgrensetilstander i henhold til Eurocode 7, eller med Kontroll av
veggstabilitet med sikkerhetsfaktorer. Beregninger av
passivt og aktivt jordtrykk er utført ved å
benytte Coulomb's teori. Beregninger av lastkombinasjoner utføres i henhold til Eurocode
2, Eurocode 7 og Eurocode 1. Seismisk last
av jordtrykk er beregnet med teorien av Mononobe-Okabe. (Eurocode 8, Del-5). Tilleggslaster for jordskjelv er horisontale og
vertikale seismiske krefter fra massene av konstruksjonen ifølge Eurocode 8, Del 5.
|
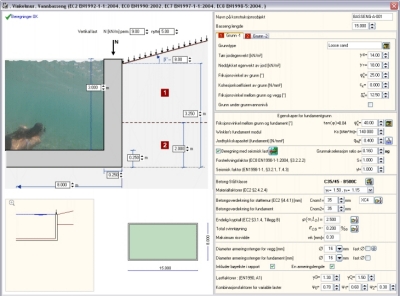 |
Vannbasseng,
svømmebasseng (2015)
Beregninger for rektangulære vannbasseng.
Dimensjonering for 2-Dimensjonalt tverrsnitt i bassengets kortside
(bredde).
Hoveddimensjoner er bredde av basseng B [m] ,
lengde av basseng L [m], og bassengdybde H [m].
Bassenget er antatt å stå på elastisk grunn og
er analysert med elementmetoden. Bassengvegger er delt i to
bjelkeelement med lengde H/2. Bassenggulv er modellert med 16
bjelkeelement med knutepunkt til grunn med elastiske fjær. Stivheten
til elastiske fjær er beregnet fra Winkler’s fundament modul, Ks [kN/m2/m].
Alle lastforhold er inkludert ifølge Eurocode 0,
(EQU,STR, og GEO) for:
- Tomme vannbasseng (kun jordtrykk),
- Fylte vannbasseng uten jordtrykk
- Fylte vannbasseng med jordtrykk
Dimensjonering av armert betong inkluderer også
krav for bruksgrensetilstand med rissanalyse og kontroll, rissvidde
spesifisert fra bruker. |
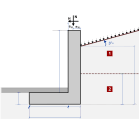 |
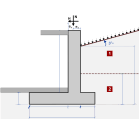
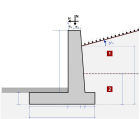
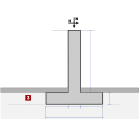
Kjellervegger (2015)
Det er to typer kjellervegger.
I det første tilfellet er utgliding hindret på
grunn av grunnplate. Det aktive jordtrykk er som vanlig beregnet med
Coulomb’s (1776) or Rankine’s (1857) teorier. Eurocode 7,
§ 9.5.1.
I det andre tilfellet, når veggens topp også er
hindret horisontal bevegelse, er det horisontale jordtrykk i
hviletrykkondisjon (Ko), i henhold til to Jaky’s (1948) , Eurocode
7,
§ 9.5.2.
Dimensjonering av armert betong inkluderer også
krav for bruksgrensetilstand med rissanalyse og kontroll, rissvidde
spesifisert fra bruker.
|
|
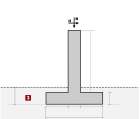
Bærevegger
(2015)
Bærevegger med vertikal eller horisontal last på
topp uten jordtrykk. Den horisontale lasten på topp kan defineres
fra Eurocode 1, 1-1:2001, Tabell 6.12
I henhold til Nasjonalt Tillegg, og byggets
bruk, er vanlig verdier qk~ 0.50 to 1.00
(kN/m2)
Den horisontale lasten på toppen kan også defineres ifølge Eurocode
1, 1-7:2006, i tilfelle ulykkeslaster.
|
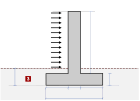 |
Vegger med jevnt
fordelt horisontallast (2015)
I tilfelle
vindlast er vindtrykket i henhold til Eurocode 1, 1-4:2005. |
|
 |
 Konsoller KonsollerKonsoller beregnes
ifølge Eurocode 2, § 5.6.4,§ 6.5, og Annex J.3. Konsoller med 0.40<=ac/hc<=1, beregnes
med en enkel stavmodell basert på strekkstaver og trykkfelt/trykkstaver.
Konsoller med ac/hc<0.40 beregnes med å benytte hc=2ac. Konsoller med ac/hc>1 er beregnet
med teorien strekkteori, i likhet med utkragerbjelke.
Betongens bærende
trykk, under bæreplate, er kontrollert for å ikke være større enn 0.60 Fcd.
Lastkombinasjoner
i henhold til Eurocode 0 og 1. |
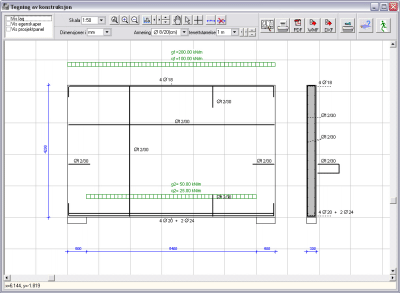 |
 Høye bjelker Høye bjelkerHøye bjelker med dimensjoner Leff/h<=2, hvor Leff
er lengde og h høyde.
Beregningsmetoden for høye bjelker er
basert på elastiske materialegenskaper. Beregningsmodellen, en enkel
stavmodell basert på strekkstaver og trykkfelt/trykkstaver.(Eurocode
2, § 5.6.4).
|
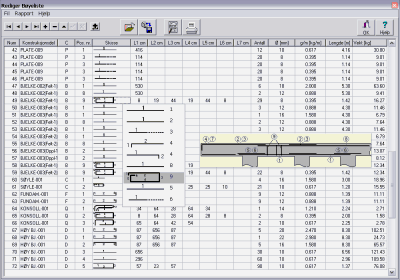 |
 Bøyelister BøyelisterDetaljerte bøyelister produseres samtidig
med rapporten. I bøyelistene inkluderes alle konstruksjonsobjektene som er valgt.
Rekkefølgen av objektene kan også justeres.
Du kan enkelt redigere og oppdatere
bøyelistene med nedtrekksmenyer. |
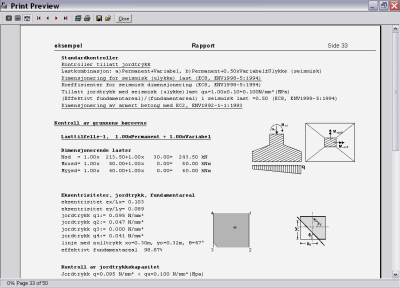 |
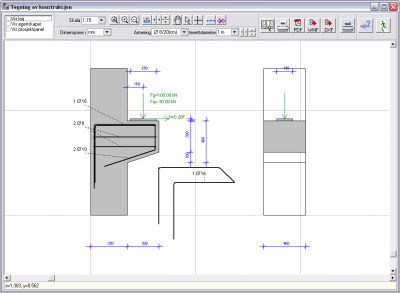
 Vis rapport Vis rapportRapporten viser i detalj
alle kalkulasjoner og beregninger trinnvis med referanse til korresponderende
beregningsregler. Rapporten inneholder også
oppriss, grafer og formler. I tillegg kan bruker spesifisere tittel, logoer og font.
Ved forhåndsvisning av rapporten vises alle objekter som er markert
 i vinduet med
konstruksjonsobjekter. Du kan enkelt justere rekkefølgen av objektene i rapporten. i vinduet med
konstruksjonsobjekter. Du kan enkelt justere rekkefølgen av objektene i rapporten.
Rapportens tekst kan eksporteres til fil i
Word format. |
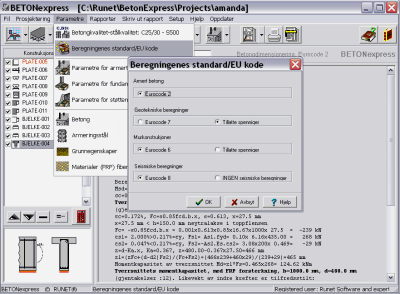 |
 Parametere-Beregningsregler Parametere-Beregningsregler
Alle parametere er innstilt i henhold
til den nasjonale standard som velges. Når du velger NA for Norge,
er alle beregningsparametre er satt i henhold til EN-NS. Om du
ønsker å forandre parametere, kan velge andre beregningsregler
dersom du ikke benytter Eurocode med nasjonal standard:
Du kan velge kombinasjoner av beregningsregler:
- Armert betong - I henhold til Eurocode 2 eller Nasjonal
standard (dersom tilgjengelig)
- Geotekniske beregninger for fundament og støttemurer - Beregninger
med Bruddgrensetilstander i henhold til Eurocode 7 eller Beregninger med tillatte
spenninger.
- Prosjektering av gravitasjonsmurer - Beregninger med
Bruddgrensetilstander i henhold til Eurocode 6 eller Beregninger med tillatte spenninger.
- Seismisk beregning - Seismiske beregninger ( i fundament og
støttemurer), i henhold til Eurocode 8 eller Ingen seismiske beregninger.
Parametre for beregningsregler og forhåndsvalgte verdier kan
justeres og innstilles av bruker. |
  |
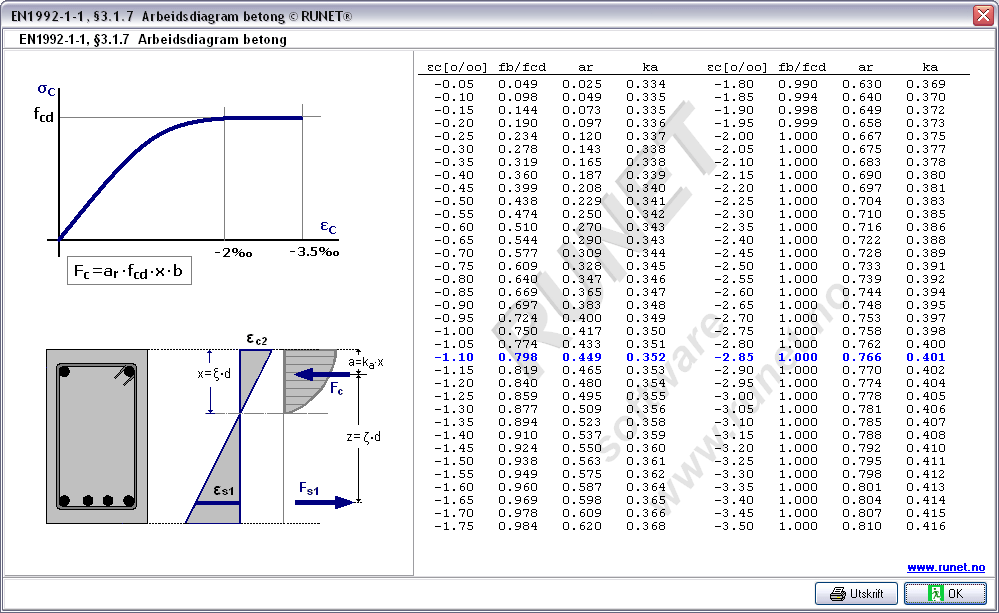
 EC2 Tabeller og diagrammer
EC2 Tabeller og diagrammer
Materialer -
Betong - Stål
Kapasitet
av tverrsnitt
- Kapasitet
for bøyemoment av platetverrsnitt
- Kapasitet
for bøyemoment av bjelketverrsnitt
- Kapasitet
for bøyemoment av bjelketverrsnitt med flens
- Kapasitet
av søyletverrsnitt
-
Skjærkapasitet
Bøyningsdiagrammer
-
Bøyedimensjonering Koeff. Kd, ks
-
Bøyedimensjonering Koeff med, w
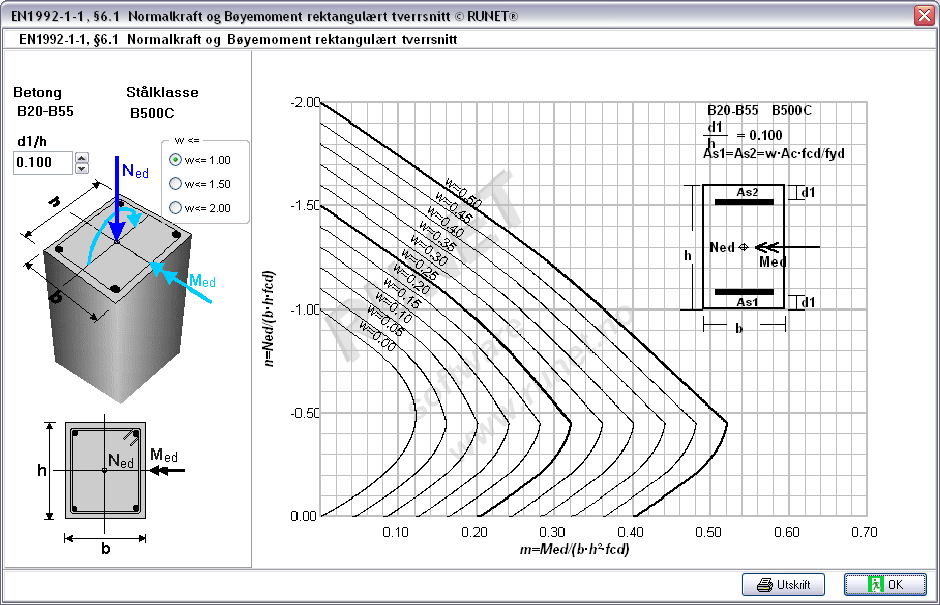
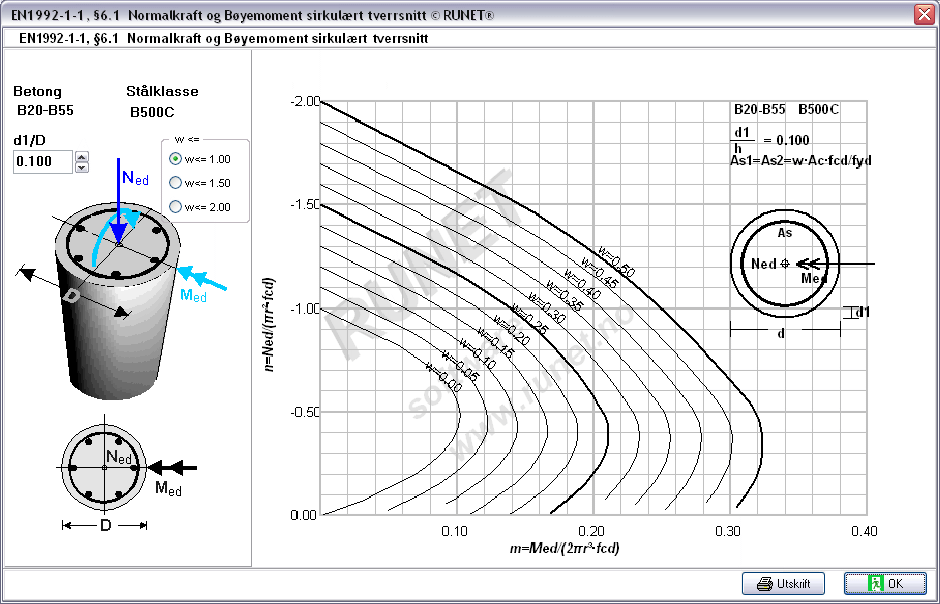
Diagrammer søyler
-
Normalkraft og Bøyemoment rektangulært tverrsnitt
-
Normalkraft og Bøyemoment sirkulært tverrsnitt
- Biaksial
bøyning rektangulært tverrsnitt
|
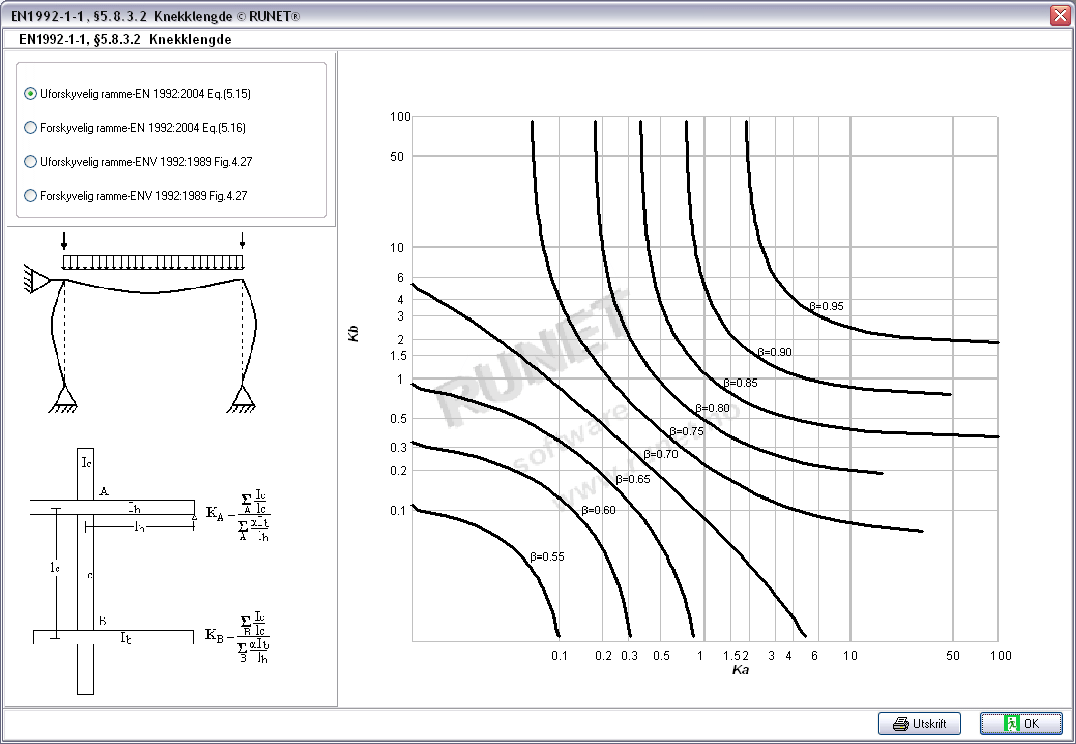 |
Diagram,
Knekklengder for rammesøyler
-
Knekklengde
- Diagram,
Kontroll av nedbøyning
|
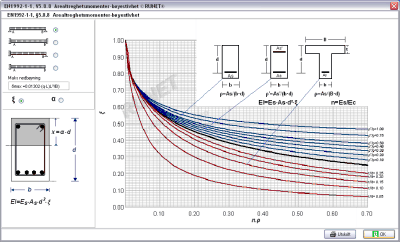 |
Arealtreghetsmomenter-bøyestivhet |
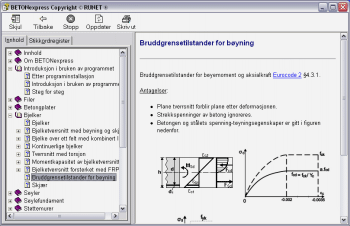 |
 On line
hjelp On line
hjelpEt innholdssensitivt
Hjelp system, guider deg gjennom bruken av programmet og Eurocode reglementet.
 Brukermanual
inkludert Brukermanual
inkludert
Online
brukermanual i pdf format. |
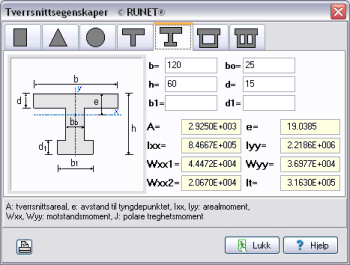 |
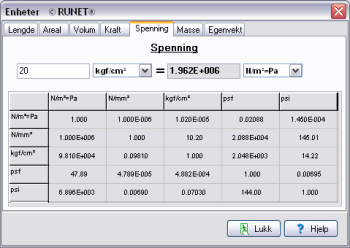
 Ingeniørverktøy IngeniørverktøyNyttige redskap for ingeniøren.
- Omregning av
enheter
- Beregning
av Tverrsnittsegenskaper
- Arealberegninger
- Stålprofiler
- Jordtrykkskoeffienter
|
 |
|
|
| Revised:
desember 01, 2023. |
|
|

